6cm 表面積=4π×6×6=144π(cm 2) 体積= 4 3 π×6×6×6=2π(cm 3) 回転体の体積 回転体は、円錐や円柱、球などの組み合わせでできているので、 それぞれの部分で体積を出して足したり、引いたりする。 (例1) l 図A l 図B 円柱 円錐 半球 図Aを直線lを軸に一回転させるとS:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。底面は円なので、円錐の底面積=円の面積です。 よって三角柱の底面積=三角形の面積を算定すれば良いです。三角形の面積=底辺×高さ÷2ですね。 表面積の単位は?1分でわかる単位、表面積の意味、求め方、比表面積の読み方
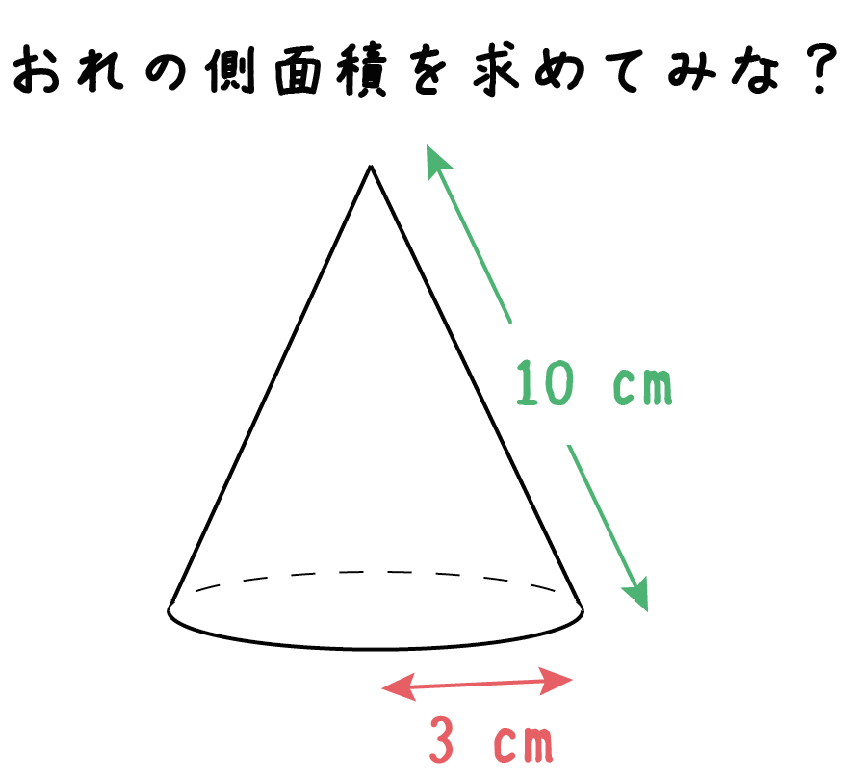
簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円錐 形 表面積
円錐 形 表面積-コーンの表面積=(22/7)7 x(7 15)=(22/7)7 x 22 = 484。 そして、コーン表面積の結果は 484センチ2 2半径25 cm、高さ9 cmの円錐形の体積を計算してみます。 議論: それに沿って半径がある円錐形の建物から知られています 25 dm そしてその全体の高さ 9 dm 続いて表面積です。 円錐の表面積の公式は「底面積 側面積」でしたね。 底面積は6 × 6 × π = 36π とすぐに出せますね。 続いて、円錐の側面積の求め方は「半径 × π(半径 母線)」でしたね。 よって、側面積の式は 6π(6 10)= 96π となります。




円錐の表面積の求め方 公式と計算例
円錐 形 表面積 円錐 形 表面積7 立体の体積と表面積 143 右の図の円錐について,次の問いに答えよ。 ⑴ 底面積を求めよ。 ⑵ 側面の扇形の中心角を求めよ。 ⑶ 側面積を求めよ。 ⑷ 表面積を求めよ。 学基本学習の基本 34 円錐の体積と表面積 問題1 右の図1 円錐曲線 円・楕円・放物線・双曲線は,何れも二次曲線であり,円錐曲線の仲間である.円錐曲線(conic section) は,下図に示す通り,円錐形をまっすぐ切った切り口の形である.例えば,円錐形の軸に対 して直角に切ると,切り口は円形となり,母線に対して平行に切ると,切り口は放物線と円錐台表面積, 円錐 円錐は、錐体の一種である。 高さを h、母線の長さを c、底面の半径を r、底面積を B (= π r 2)、底面の周を b (= 2 π r)、 と置けば、円錐の側面積 S side 、表面積 S、体積 V はそれぞれ以下で与えられる 1 : 定義
表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314円錐の表 == 立体の表面積(円柱,角柱,円錐,角錐の表面積) == 解説 立体の表面積は「展開図」で考えるとよく分かります。 右図アの立方体(正四角柱で縦横高さとも同じもの)の表面積 10×10=100(cm 2)の正方形が6個あるから 600(cm 2)・・・答 この図は、円錐を図の円柱の表面積は π (cm 2) 底面積が3 2π ,上下2つあるから18 π 底面の円周の長さが3×2× π =6 π だから側面積は6 π ×8=48 π 合計66 π (答)
四角形degf:四角形ebcg 2 右の図の abcd で、辺 ad 上に点e を ae :ed=2:1 になるようにとり、bd と ec の交点を f とします。 efd=6cm2 のとき、次の図形の面積を求めなさい。 (1) cfb (2) dfc (3) 四角形abfe 相 似⑪面積比・体積比(2)a 学 年 3年S=π× 42 −π× 22 =16π−4π=12π (答) (3) 右図のような競技場の面積を求めなさい. (答案) ____正方形の面積は (m2),半円2つ(=円)の面積は π×502=2500π (m2) だから,S=2500π (m2) (答) 注意書き π は ··のような無限に続く小数になる. 数学の答案では,正確な値 π を使って表わすことが多い.近似値(およその値)が必要になったとき円錐とは?体積・表面積の公式や求め方、展開図の作り方、計算問題などをわかりやすく解説! この記事では「円錐




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




75 Times 2 Descubre Como Resolverlo En Qanda
内面の表面積・全体容量・単重 10%さら形鏡板 21半楕円体形鏡板 指定高さの容量計算 平鏡板 単皿形鏡板 半球形体鏡板 特殊形状 円錐形鏡板 (HP)円柱 , 円錐 , 円柱と円錐の違い , 円柱の特徴 , 円錐の性質 , 円柱の展開図 , 円錐の展開図 , 『教科書 中学校 数学Ⅰ』 数研出版 『やさしくまるごと中学数学』 吉川直樹 Gakken この科目でよく読まれている 円錐の表面積を求める 展開したときのおうぎ形の中心角を求める それぞれの問題を解説していきます。 問題 下の図の立体についてそれぞれ求めなさい。 (1)この円錐を展開したときにできる側面のおうぎ形の中心角を求めなさい。 (2)この円錐の表面積を求めなさい。 体積や表面積を求める問題はよく目にすると思いますが その中でも円錐を取り上げた




円錐の表面積を 公式を使って求める チーム エン



双円錐 Wikipedia
角錐・円錐の表面積 それぞれの展開図を見て、求める面積について詳しく調べてみましょう。 角錐の場合、側面積や底面積は単純な形になり、問題ではそれぞれの縦・横、底辺・高さなどの数値が与えられるので、地道に計算していけば解けます。側面 (長方形)・・・h×2πr = 2πhr 表面積・・・2πr 2 2πhr例題4 下の直角三角形を、直線 \\(L\\) を軸として \\(1\\) 回転させてできる立体について 体積と表面積をそれぞれもとめなさい。 解説 円柱から円すいをくり抜いた立体になります。 体積 体積は




円錐の表面積の求め方 You Look Too Cool




Sqrt4d11 Descubre Como Resolverlo En Qanda
円錐の体積=底面積×高さ÷3なので 答え 096cm³ スポンサードリンク 問題③ 体積が1570cm³である次の円錐の高さを求めましょう。 (円周率は314とします。) 《円錐の高さの求め方》 円錐の体積=底面積×円錐の高さ÷3であることから円錐の表面積を、中心角を使って求める まず、円錐の展開図は「円+おうぎ形」という形になる。 展開図を描く段階では、おうぎ形の中心角が分からない状態なので、概形(だいたいの図)で問題ない。 さて円錐の表面積の求め方は少々長いが、理解し 円錐の表面積=円の面積+扇形の面積 となります。したがって、これを求めるには、円の面積公式と扇型の面積公式を利用すれば良いのです。 円錐の底面積 本問における底面積は、半径が2の円の面積を求めること、ということになります。 =4π




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
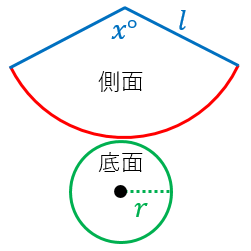



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru_1_幾何I_本冊2章smd Page 19 17 v340 166 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 167 右の図は,直方体から円柱の半分を切り取った立体である。 この 立体の体積と表面積を求めよ。 168 右の図は,縦6cm,横8cmの長方形から,1辺4cmの正方形を図の円錐は底面の半径が5cm,表面積が60πcm 2 である。この円錐の母線の長さを求めよ。 右の図のサッカーボールは、12個の正五角形と個の正六角形の合わせて32面でできた多面体である。どの頂点にも1個の正五角形と2個の正六角形の面が集まっている。




角錐 円錐の体積と表面積の公式 数学fun




Tossランド 角錐 円錐の表面積
A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 円錐の表面積の求め方の公式 って知ってる? 円錐の半径をr、母線の長さをLとすると、円錐の表面積はつぎのように計算できちゃうんだ。 πr(L+r) まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 側面積 $$8\times 3\times \pi=24\pi(cm^2)$$ 底面積と側面積がそれぞれ求まれば、あとは合計すれば終わり。 表面積




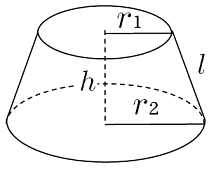
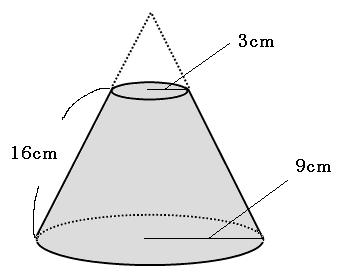
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円すいの展開図 表面積の求め方 公式があるの知っていますか
円錐の表面積は、母線×底面の半径×π+底面積なので、12×(10÷2)πで求められます。 なので側面積は、60π㎠です。 底面積は10÷2πなので5π㎠です。 したがって、表面積は(60+5)πで65π㎠です。 底面 半径 600 高さ 300の円錐形です。 底面の中心から水平方向に150離れた線で、高さ方向に垂直に切り取ります。 切り取られた立体の側表面積を教えてください。 できるだけ簡潔に、円錐台の表面積 底面の面積 $\pi a^2$ 天面の面積 $\pi b^2$ 側面積 $\pi(ab)\sqrt{(ab)^2h^2}$ を足し合わせると、円錐台の表面積が求まります。 次回は チェバの定理の覚え方、例題、証明、逆 を
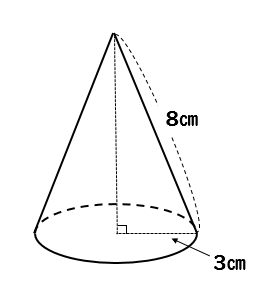



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
双円錐(そうえんすい、bicone, dicone)または重円錐(じゅうえんすい)、両円錐(りょうえんすい)とは、2つの合同な(直)円錐を底面同士で貼り合わせた立体図形である。 張り合わせ面を赤道面という。 ただし赤道面は、(底面が円錐の面であるというような意味では)双円錐の面ではない。直円錐の半径と高さから体積、側面積、表面積を計算します。 斜切円錐の体積 斜切円錐の体積 直円錐を斜めに切断した体積と切断面積と底面積を計算します。




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




角錐 円錐の体積と表面積の公式 数学fun



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー




角錐 円錐の体積と表面積の公式 数学fun




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル




公式を図解 すい体の体積 円すいの表面積の求め方




毎日問題を解こう 27 苦手な数学を簡単に




円錐の表面積の求め方 公式と計算例
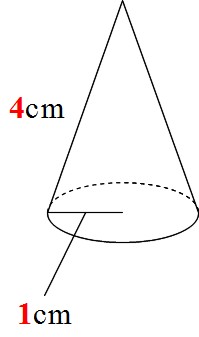



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo




5 9 Times2 118 Descubre Como Resolverlo En Qanda




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中1数学 円錐の裏技2つ 中学生 数学のノート Clear




円錐の表面積 あんず学習塾のメモ 図表置き場




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3



3




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の表面積 あんず学習塾のメモ 図表置き場




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



1




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




2 の円錐の側面積の式の意味が分かりません Clear




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順



初等幾何 円錐台の側面積を求める 大人が学び直す数学




3d100 See How To Solve It At Qanda




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積 Youtube




円すいの展開図 表面積の求め方 公式があるの知っていますか



円錐とは 体積 表面積の公式や求め方 受験辞典




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




円錐の表面積の求め方 公式と計算例




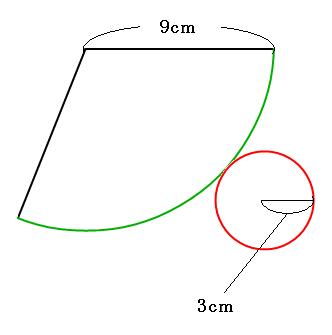
数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



Q Tbn And9gcrusy9q05tdqbvky0jdxai8wca17tshehucrhrk Jyhrqfhrucy Usqp Cau




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




公式を図解 すい体の体積 円すいの表面積の求め方




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円錐とは 体積 表面積の公式や求め方 受験辞典




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




角錐 円錐の体積と表面積の公式 数学fun




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張
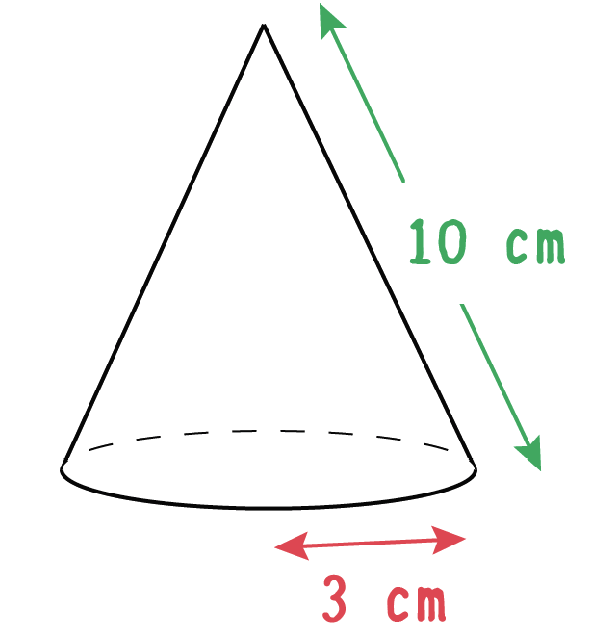



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



中学数学 円すいに関する練習問題
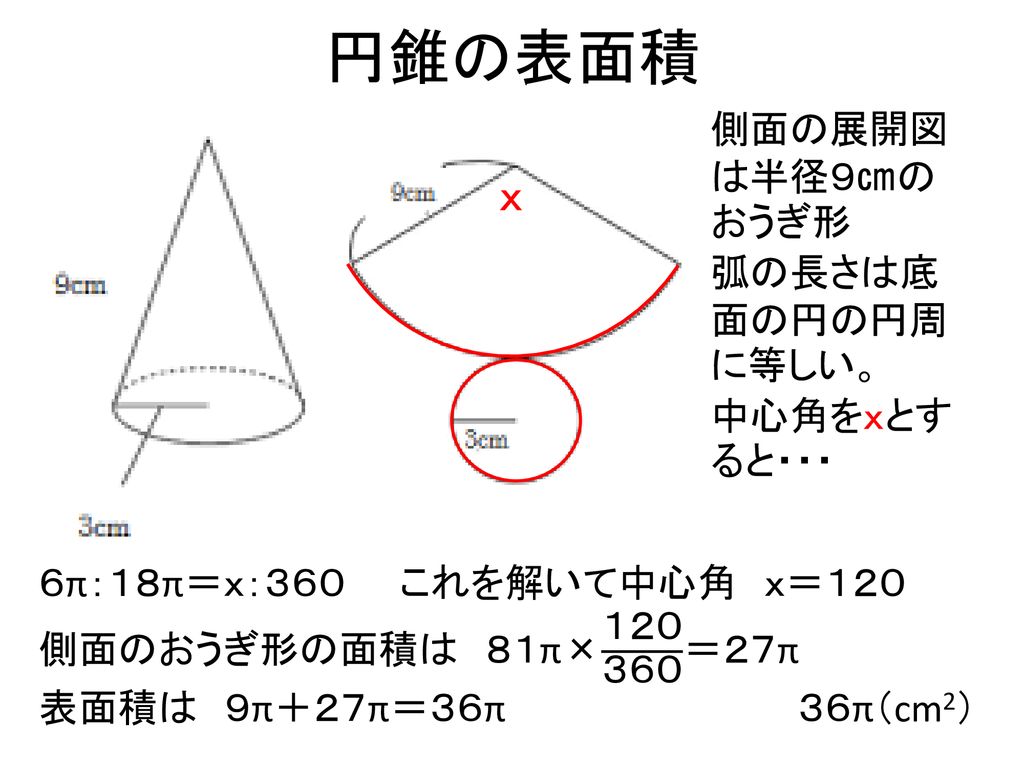



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download




中1数学 円すいの問題 練習編 映像授業のtry It トライイット




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
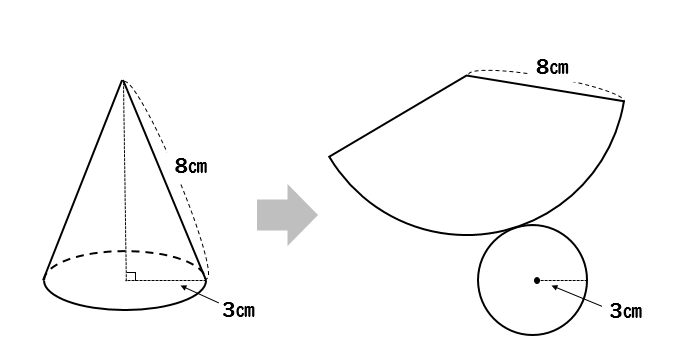



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




Descubre Como Resolverlo En Qanda



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋




円錐の表面積のやり方を忘れてしまいました 1問でも良いのでお願いします Clear




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



円錐の側面積だけを求めるときは中心角を使って 円錐の表面積の側面 Yahoo 知恵袋




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐の表面積 あんず学習塾のメモ 図表置き場




中3 三角形の相似 円錐の体積比 日本語版 Youtube




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
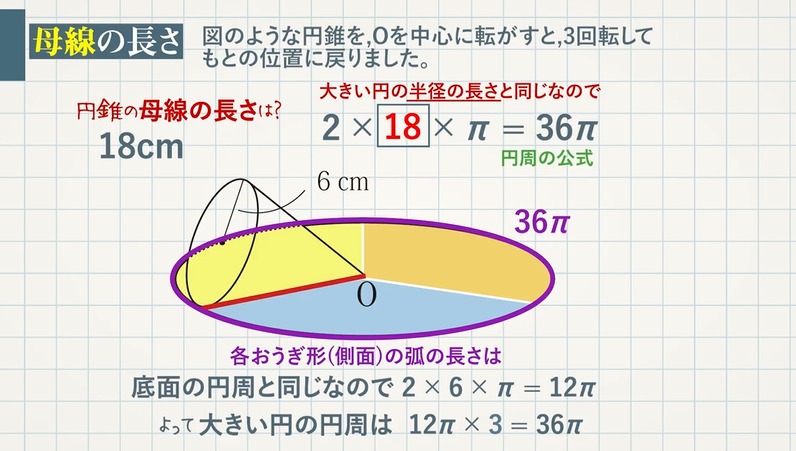



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の表面積を 中心角を使って求める チーム エン




切り取られた円錐形の表面積 底面 半径 600 高さ 300の円 Okwave
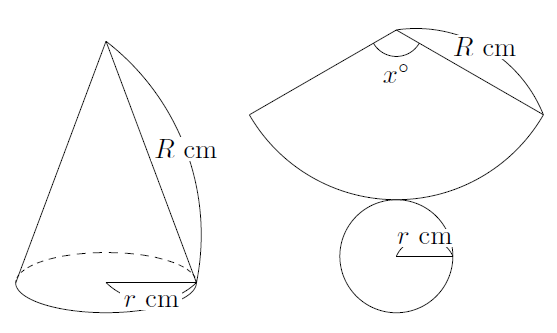



角錐 円錐の表面積 まなびの学園




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




円錐の体積ってなんであの公式なの Webty Staff Blog




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の表面積 Youtube




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例




公式を図解 すい体の体積 円すいの表面積の求め方



円錐とは 体積 表面積の公式や求め方 受験辞典




角錐 円錐の体積と表面積の公式 数学fun




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
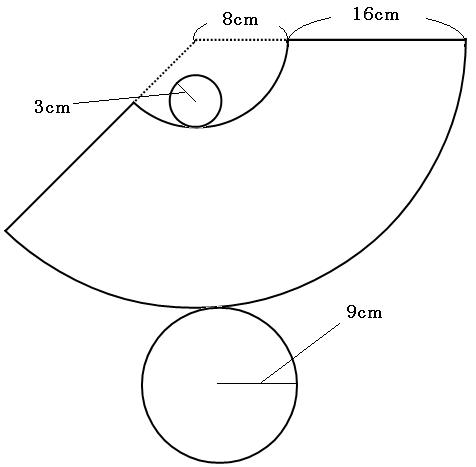



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる
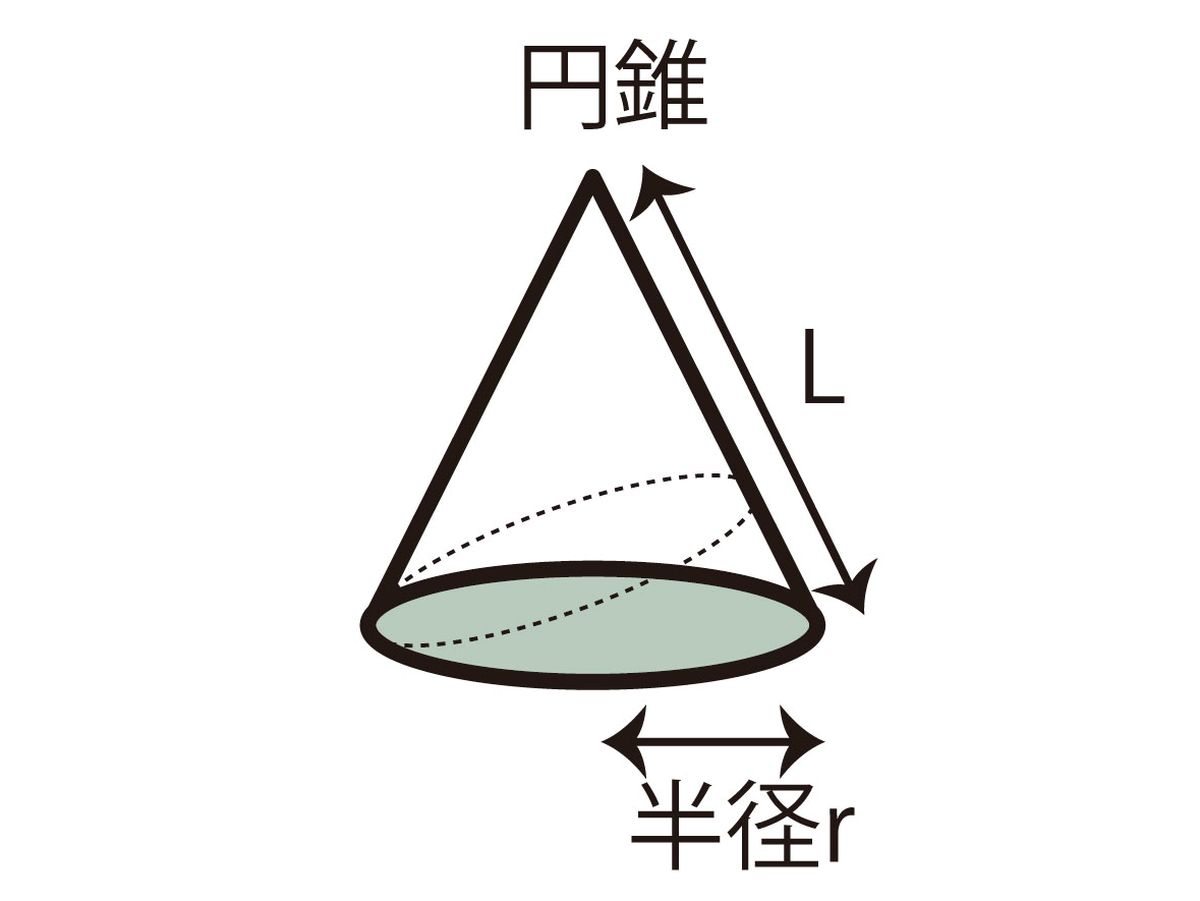



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com


